Happy New Year, Code Wolfpack, and welcome back to the Decentralizing the Database series. If you missed the previous two parts in this, I’d definitely recommend catching up with Part 1 and Part 2. Today we’re going start off right where we left off, and venture into somewhat unchartered terrain in the world of computing: the unification of time and space.
A Wrinkle in Time
When we talk about the notion of time, a lot of us take the tooling, infrastructure, and standards put in place for decades (and millennia on some matters) for granted. Let’s take an extremely simple scenario into consideration – two machines, every seven minutes, alternating sending each other a “ping” message:
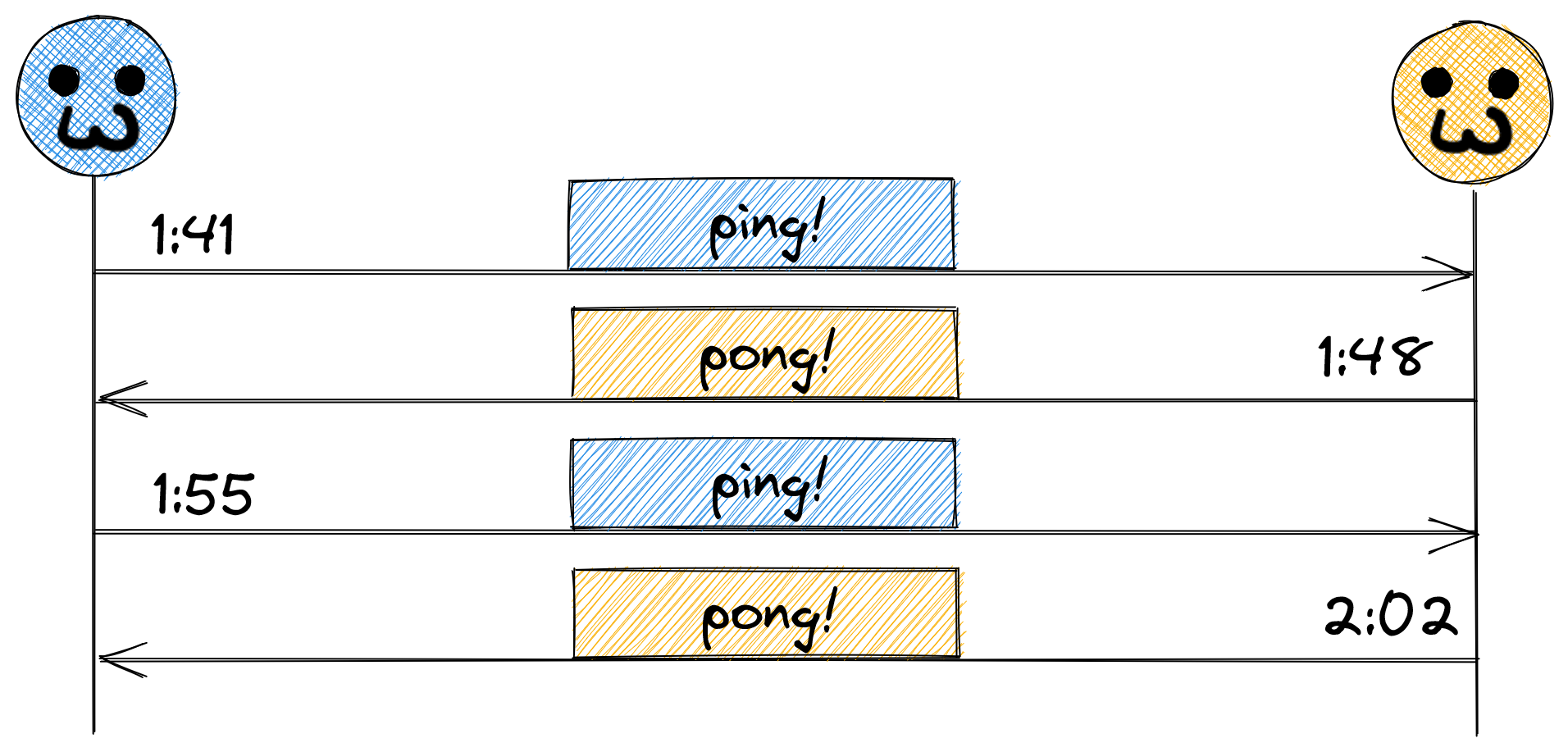
And this is all well and good, except, how did they agree on that cadence? Did they use a running timer, kicking off a ping every seven minutes, or did they use the system time? What happens if they didn’t choose that same basis? Take the scenario where the one on the left used a running timer, but the one on the right used the system clock. Assuming the system clock is accurate, things should stay in sync, right? What about daylight savings?
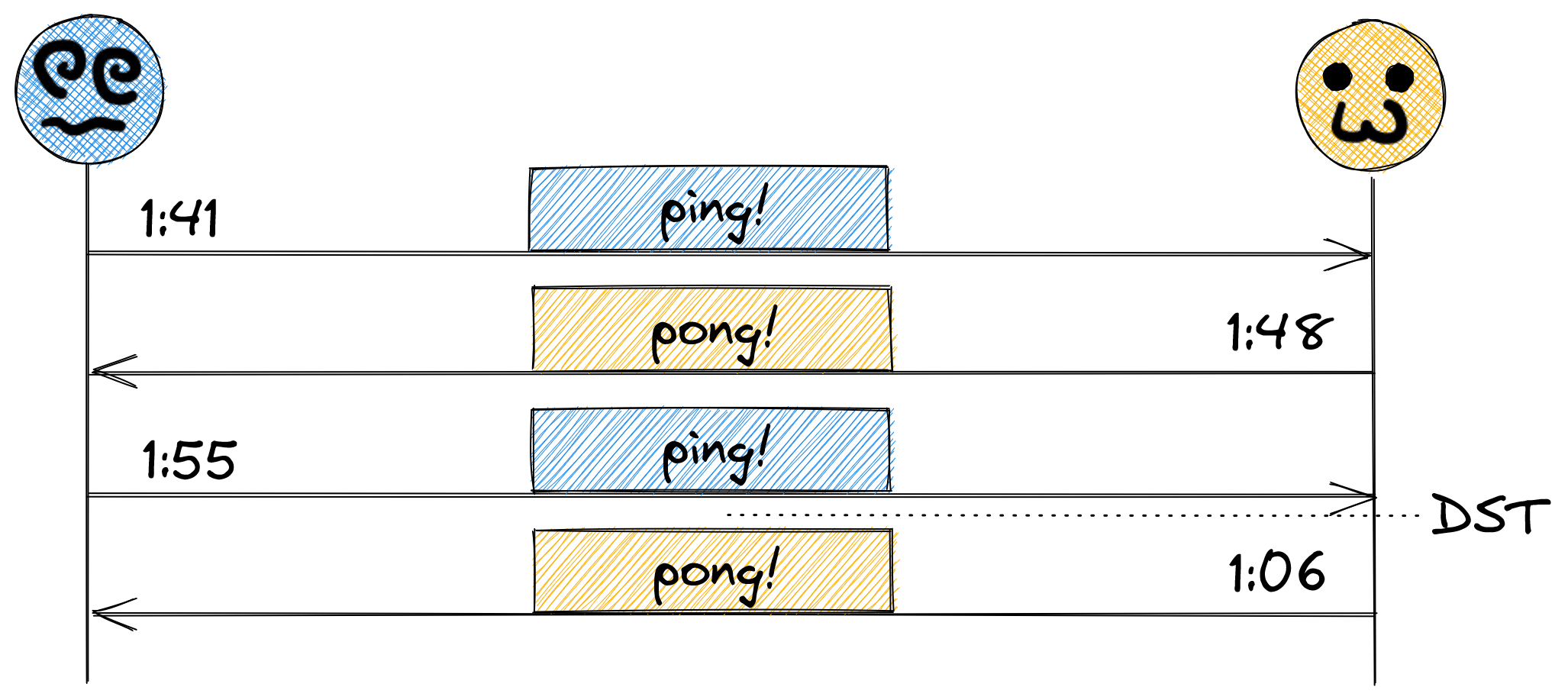
Going back an hour reset the cadence by an hour, and since seven minutes doesn’t fit neatly in the 60 minute period of an hour, it went out of sync. And this is just a simple scenario – assuming time will stay in sync without considering clock drift, different NTP servers (or lack thereof), regional differences in time zones, and so many more incorrect assumptions are things that will invariably come to bite you in your career as an engineer.
The Fault of the Generals
Researchers have spent countless hours in getting distributed systems to agree on time. Google, for example, has gone as far as to set up atomic clocks and GPS antennae (for fault tolerance) for their Spanner database. This helps insure there are no unexpected surprises like agreements to add leap seconds, but this only works under situations where there is a central authority – Google owns their database and infrastructure, so they can be their own arbiter of time for their database. So how do you come up with the right time when nobody agrees? This question is actually best answered with another question: Why do we care about time at all?
In the above scenario, we described a simple ping cadence back and forth. These two parties would want to be in sync, because their protocol is intended to be cooperative. But what if we’re in an environment that is competitive? Or worse, fully adversarial? Take the scenario in which a server is running a contest. First party to ping at exactly midnight is the winner, getting a $100 cash prize. In a perfect system, the server has a trustworthy source for time. But let’s say that we can’t trust the server – they could be in cahoots with one of the competitors, and set the time to a certain offset! So to combat this, the server publishes the time as an API. So now every party is perfect calibrated against the server, offset by their latency, and can absolutely ping at precisely midnight. It’s now a fair contest, but if everyone can ping at exactly midnight, who wins? Perhaps the server can make it a random choice, but this again comes back to the prospect for collusion.
This problem exists in many places, and is only amplified when we consider one further complication: what if there is no central server, and we’re back to the peer-to-peer model? Now we have two problems: how do we sequence events, and when there are conflicting events, how do we resolve ambiguity? Both of these correspond to variations of the Byzantine Generals Problem, but their solutions require different answers. The former, is an answer of time, the latter, is an answer of space.
A Brief History of Time
The purpose of being coordinated on time, barring purely informational reasons, is to orchestrate the transition between states in a predictable way. Unsurprisingly, time’s above complications makes measurements and basis completely non-deterministic. So in lieu of time, how can we capture a reference point for stateful transitions? There are many approaches out there, let’s talk about them:
Blockchain
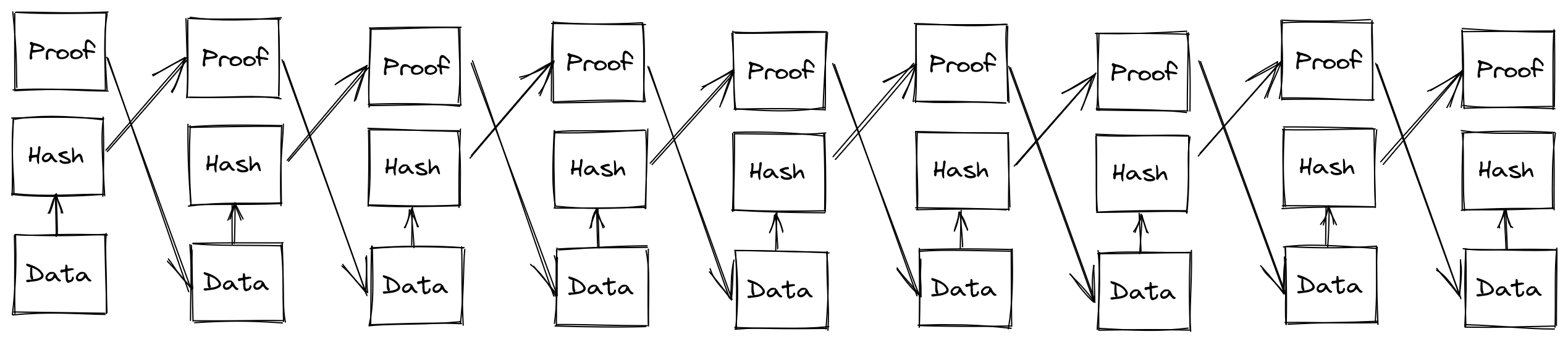
The initial Bitcoin whitepaper, and many cryptocurrencies which followed leveraged a particular structure (or variant) called a Merkle tree. This tree is produced through taking the hashes of pieces of sequential data (whether it’s a singular file split into chunks, a collection of data in a series, or independent transactions in a running ledger), then taking pairs of the hashes, and hashing those, building up to a root hash. In the case of blockchain, these snapshots of transactions are cut at some defined interval, either space or time, where then the root transaction is referenced in the next block in some way (typically in the header, but this can also be the first item in the tree). A very simplified version follows:
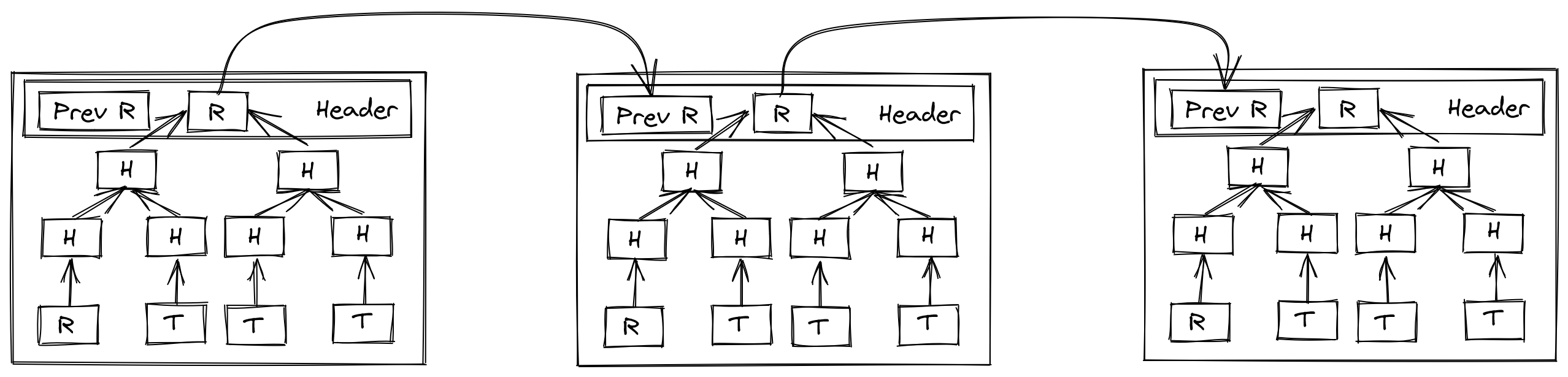
Bitcoin and many others have no notion of time at all in their structure, rather time is merely a byproduct of the network’s protocol: in the case of Bitcoin the miners collectively follow the protocol, which requires the block hash having a hash which starts with enough zeroes to meet some agreed difficulty level, the difficulty level being a collectively agreed value which calibrates to roughly issue new blocks every ten minutes. This makes strict coordination around time way less critical to get perfect, but does have its own issues: so long as the transactions do not conflict by doing so, transactions may be ordered at the whim of the miner, or even omitted from the block. Some opt for faster intervals, such as Ethereum, which aims to issue a new block every ten to twenty seconds. In the case of Ethereum, the consequence of miners being free to reorder transactions is even considered by some folks to be a feature, which leads to essentially a scheme where users can pay more in fees to have their transactions prioritized. Since the mempool in which these transactions are broadcast is publicly visible to all parties, and since Ethereum has many financial contracts on their platform which relate internally to state managed by the chain to do things like determine prices of an asset when conducting a trade, this has lead to a problem of front running, a common case being a sandwich attack where people will issue transactions which impact the price of an asset such that they can extract revenue from someone else’s trade. But despite the faults, it does seem to produce some consensus-driven approach to ordering sequences of events. Is there something we can extract behaviorally from it to get a better sense of time?
Proof of History
Solana introduced a protocol which bases the ordering of blocks on something you can see as a byproduct of a blockchain: the chaining of hashes of data in sequence. When Solana produces new “blocks” (they’re not quite blocks, but bear with me) the validator of a block is chosen in a pre-determined order. When the validator issues their block, they also issue a proof of the time spent working on the block. On the chain production side, it is unforgeably unparallelizable: even in a simple case of hashing a previous hash, you cannot produce a hash of that hash without computing the previous hash (assuming the algorithm isn’t broken). Similar to Bitcoin and others, they calibrate the speed of the “block” production to a relative standard of how quickly it takes to issue these sequential hashes on a particular configuration of server, such that a new “block” is issued every 400ms. The validation is parallelizable, as once the data sets and their chained hashes exist, they can be split and computed by a batch parallelizing processor (like a GPU) quite handily.

While in theory the high speed of streaming transactions would make it much harder to produce bots watching out for front-runnable transactions, it does miss the possibility that a front-runner could be the validator themselves. Solana and others attempt to make up for this possibility of a malicious validator by rotating the leader validators around at the 400ms interval. This has its own drawbacks, in particular: network outages, upgrade coordination, and significantly additional effort required to be spent by all validators even when not the leader. But lets assume all we care about is just having a viable substitute for time, a substitute in fact, that needs to not only be produceable on a mobile device, but many substitutes which may need to be verified in parallel on a mobile device. At that point, the hash chaining approach is not sustainable. Is there something even further we can extract behaviorally from it to get a better sense of time?
Verifiable Delay Functions
When you distill the elements of proving a period of time has passed, the core components could be thought as three distinct problems to solve: Establishing agreed parameters (such as the duration you wish to prove has passed), computing that proof, and verifying that proof. Boneh, Bonneau, Bünz and Fisch produced a formalization of this problem along with some approaches, which was later extended with more performant approaches by Wesolowski and Pietrzak. An approach using supersingular isogenies enables an ideal VDF in terms of the problem space, with a very stark downside: the setup phase requires a trusted construction. Thankfully, the Wesolowski construction does not, but still has very agreeable performance for validation. So let’s dive into that.
VDF from IQC, made EZPZ
I’m afraid compared to the last post, the option for visual explanations is pretty limited, but thankfully it won’t be too big of a leap if you got the elliptic curve math down pat. Recall from the previous session where we discussed the notion of finite fields and their order, and how this relates to elliptic curves. As I suggested, there are many systems which possess the properties which enable addition and multiplication.
Enter Imaginary Quadratic fields. In elliptic curve cryptography, the private key was some random scalar, the scalar multiplication of this value against the pre-agreed generator G was the public key, and the order of the field is part of the public parameters. For IQ cryptography, the private key is the order itself, as efficiently calculating the order of a class group is assumed to be computationally hard. This group’s description is effectively the public key. What can we do with this?
Consider a simple problem: In elliptic curves, the multiplication of a scalar against a point is repeated additions of that point, which means it is likewise possible to exponentiate: kG, where k = 2**x. If you could ensure that the individual tasked with calculating this doubling were actually doing so, rather than just calculating k first and then conducting the scalar multiplication, you’d have a very solid and predictable VDF. That being said, while determination of a scalar given a point and its generator is intractible, multiplication of that scalar is quite efficient, in part because we know the order of the group. But what if we don’t? This is where the same arithmetic laws being applicable, but in the domain of IQC, make this problem not only applicable, but a very good VDF, as the verifier simply needs to have the secret key and can verify the proof efficiently. This is an extreme simplification of how the process works, as this construction implies an two-party interactive protocol (i.e. the verifier must provide parameters to the prover, then the prover must send this back, verifier accepts/rejects), and does not admit other parties to succinctly verify the value, so there are further constructions that essentially produce a result value and a proof value which reduces the burden for the validator in confirming the result to logarithmic time, keeping the need for fast verification relatively in check.
A Stitch in Time
If we incorporate within the proof basis some kind of precursor information, such as a block hash, we now have a fundamental construction for a true proof of history model, but which is efficiently verifiable. A verifiable proof of history essentially allows us to maintain a weaving pattern that gives us a few nice additional properties:
- The protocol can efficiently reward the prover and the validator for their work
- A validator can efficiently validate multiple proofs, preventing the “catch-up” problem seen on networks using a hash chain, plus enabling parallel block stream processing (if applicable)
- The VDF also serves as a randomness beacon, which can be used for additional network purposes
The War of Time and Space
With a VDF as a backbone to track time and provide a randomness beacon, we now have a signal of two valuable otherwise non-deterministic properties that we can pump through the infrastructure, providing referenceable order to events. This brings us to the first major overture of the Quilibrium composition: block storage over time. How does this relate to our VDF? Assume some block of data we wish to prove is available to a collection of validators. Calculate the HMAC of the block, using the block as m, and a signature of the randomness beacon for K. This is your new input for the VDF proof basis. Ensuring that the block size is sufficiently larger than the theoretical bandwidth required to re-download, issue a VDF proof within the window, and then lose the file again essentially secures against a bad actor pretending to store the block but only retrieving it on demand. Keeping the VDF stream for proof separate from the central history backbone VDF enbales parallelism for either multiple providers of the same data, or multiple providers of multiple blocks of data. This is all well and good, except when you add incentives to the mix. A malicious prover could simply generate two keys to use for signing the randomness beacon and calculate two HMACs for the VDF and run in parallel, being rewarded twice over. How do we distinguish between two honest provers and a dishonest prover in parallel? Each prover must store the copy in encrypted form, and calculate the HMAC of the encrypted block, providing the encrypted block and key on demand instead of the plaintext. To optimize for flexibility in storage medium, availability, bandwidth, and further usage potential, the block size itself would be limited to 256kB.
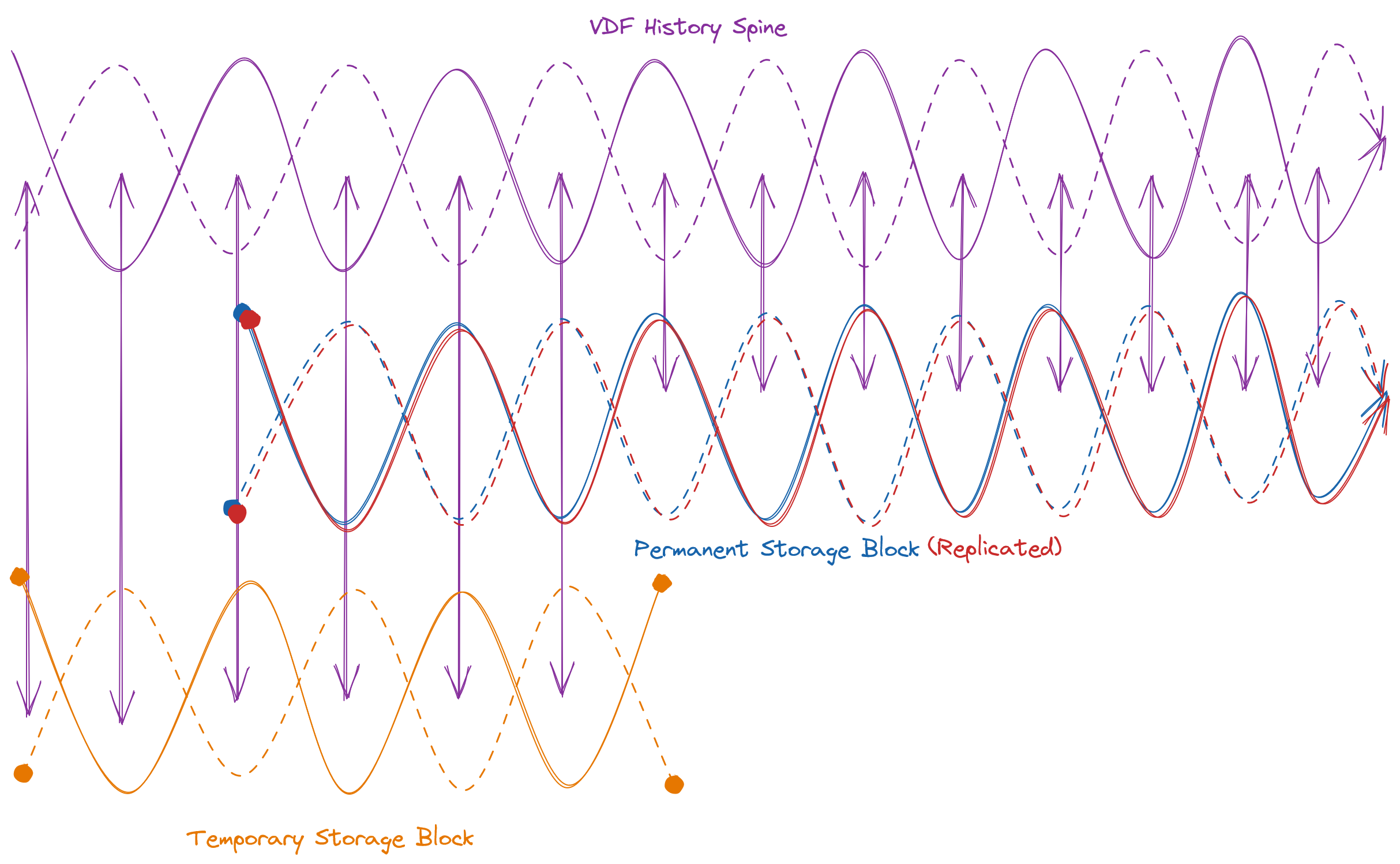
Further usage? What could I mean by this? And wait a minute, what exactly are we storing? And how is this being encrypted? Let’s not get ahead of ourselves – everything in their proper time and space: Part 4.
 Code Wolfpack
Code Wolfpack